Convolutional Neural Network is a efficient tool to handle image recognition problems. It has two processes: forward propagate and backward propagate. This article focus on the mathematical analysis of the forward propagate process in CNN.

Input Layer

Convolution of one filter in input layer

This part focuses on the convolution process of one filter in the input layer. Our image size is 256*256 pixels. The input image of CNN is gray and has only one channel: L channel. So the filters of this layer has depth of 1. For the purpose of clarity, we call this input channel “input volume”, and its size is 256*256*1. Similarly, the “volume size” of filters in this layer is 3*3*1.

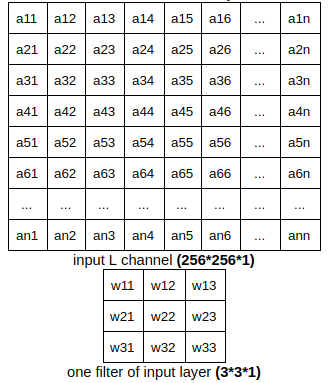
This filter will go through the this input volume and compute convolution along the way. The convolution result will be stored in a new table. For the purpose of clarity, we call this output table: “slide”.

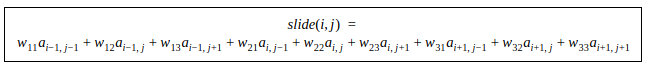
This can be computed easily by numpy:

slide(i,j) =numpy.tensordot( filter_volum, cor_part_of_input_volum,2)

The stride of inner layer is 1. Before convolution, we need padding. Because if not, the size of this slide will be 2552551. But our final output needs to be the same as the original size of our input which is 256*256. By padding 1 pixel, we can keep the size of this slide unchanged.

Numpy has padding function. Use the following to pad 1 pixel by constant number: 0.

padding = numpy.pad(input_volum, 1,'constant')

Convolution of all filters in input layer

Suppose the input layer has 64 filters. Each of these filter goes through the input layer and get one slide using the function mentioned above. So we have 64 slides. The size of each slide is 2562561. Stack these 64 slides one in front of another, and get a volum, whose size is 25625664. This volum is the output of this convolutional layer.

64 filters ---> 64 slides ---> volum of depth 64 

Inner layer

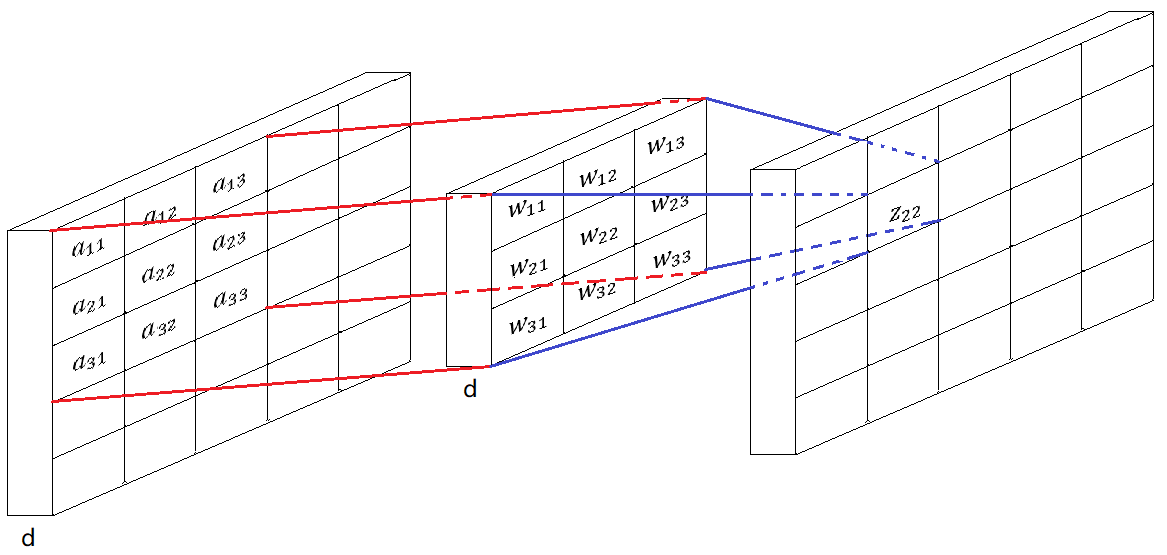
(d>1)

The difference between inner layer and input layer is the depth. One inner layer take “the output volume of the former layer” as its input. The depth of its input volume is d (d>1) . The depth of filters in this layer is equal to d.

slide(i,j) =numpy.tensordot( filter_volum, cor_part_of_input_volum, 3)

Another difference is strides. If the input volume of an inner layer is nnd, and it has m filters. Then the size of each filter is 33d. The output volume of this inner layer (1 pixel padding) will be the size of:

• If the stride of this layer is 1: n*n*m
• If the stride of this layer is 2: (n/2)*(n/2)*m

Upsampling layer

This layer does nothing but upsampling its input volum through “nearst neighbor upsampling”. For example, take each slide of the input volume as follows:

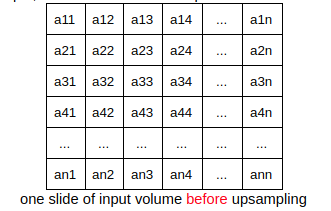
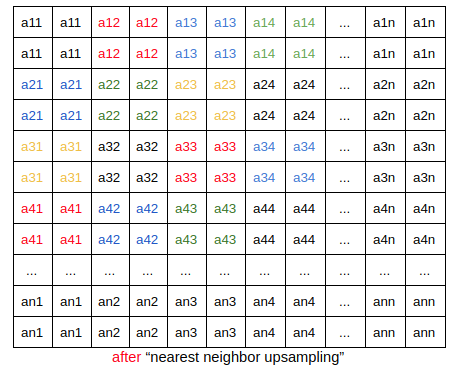
For each slide of the input volume, repeat the above process. So the size of output volume of this layer is 4 times larger.

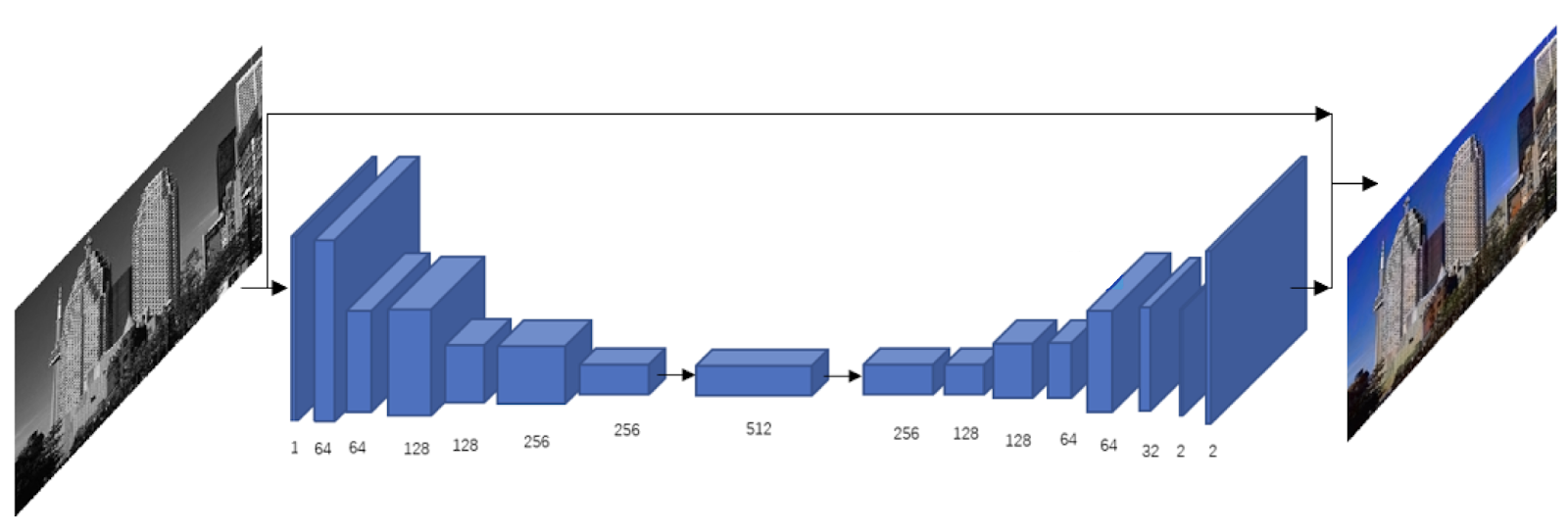
The following picture shows the structure of this CNN.

• After several steps of convolution, the length and height of our volumes decrease and the depth increase. The information on this image is merged and combined.
• Through upsampling process, we can restore the size of input images

Next post we will look into the back propagate process in CNN.